Do smoother areas of the error surface lead to better generalization?

This blog post was originally published on Medium on 11/07/2017.

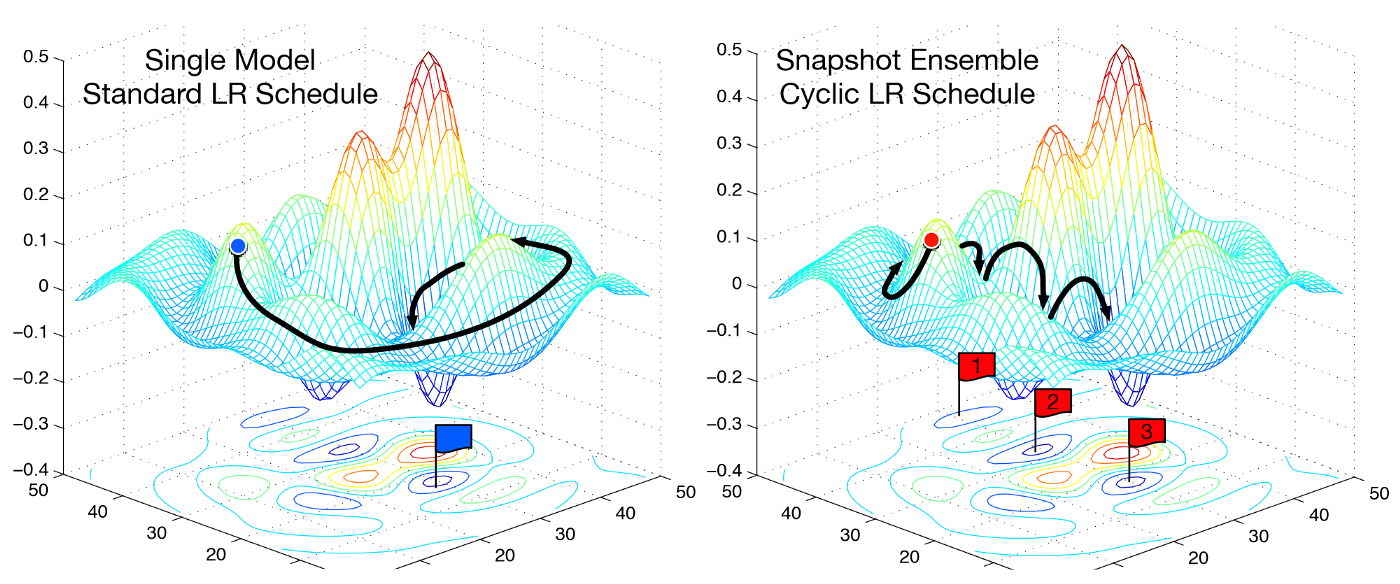
In the first lecture of the outstanding Deep Learning Course (linking to version 1, which is also superb, v2 to become available early 2018), we learned how to train a state of the art model using very recent techniques (for instance, the optimal learning rate estimation as described in the Cyclical Learning Rates for Training Neural Networks paper from 2015).

While explaining stochastic gradient descent with restarts,

Jeremy Howard made a very interesting point — upon convergence, we would like to find ourselves in a part of the weight space that is resilient, meaning where small changes to the weights do not cause big changes to the loss.

This led to a very interesting discussion on the forums, which was prompted by me wondering why we care for the surrounding area of the weight space to be resilient — after all, isn’t low loss the only thing that we really care about?

Jeremy Howard made a comment that left me pondering for quite a while and ultimately blew my mind when I understood it:

We only care about loss in the validation/test sets. But our training set can’t see that data. So we need to know whether slightly different datasets might have very different losses.

A-ha! The presupposition is that by looking at the error surface surrounding our solution we can tell something about its ability to generalize! And all of this happens by looking only at the train set!

Intuitively, this makes a lot of sense. But can we indeed demonstrate this effect? Let us run an experiment (accompanying keras code) and find out.

The setup

I trained 100 simple neural networks (each consisting of a single hidden layer with 20 units) on the MNIST dataset achieving on average 95.4% accuracy on the test set. I then measured their ability to generalize by looking at the difference between the loss on the train set and the test set.

Once a model was trained, I randomly altered its weights by small amounts and I evaluated it on the entire training set again. The idea is that should the surrounding weight space be smooth, the difference in loss will be small. On the other hand, if we find ourselves in an area that is spiky, the difference will be large. I took 20 such measurements for each model that I trained.

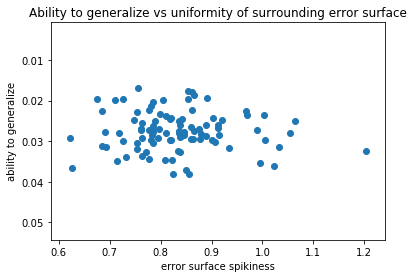
What I am hypothesizing is a linear relationship between the smoothness of the surrounding area and the ability of a model to generalize.

Unfortunately, this is not the story that the data is telling me:

Summary

Can we safely conclude that the relationship we hypothesized does not hold? By all means, we cannot do this either!

There is a lot of other things that could be interfering here. For instance, it could be the case that the dataset is so big relative to its complexity that when a simple model is nearly completely trained all the solutions are equivalent and the differences in their ability to generalize become meaningless.

Or it might be that the measure that I use for estimating the spikiness of the surrounding area is inadequate — the step size might be too small or too big or the number of measurements taken per each model might be too small to capture anything but noise.

I also wonder what batch normalization does to an error surface on a simple dataset such as this — it might be effectively flattening it out to the point where observing significant differences in smoothness becomes infeasible.

All of this is nothing but interesting food for thought at this point as I have no data to back any of the notions. Now that I see how rich this area can be, I wonder if there is any literature that would explore this further.

I am also tempted to run a couple more experiments. But first things first! I cannot express how valuable the material shared by Jeremy Howard and Rachel Thomas is. Till the course is in session, that is where my energy should be. Who knows how many thought provoking ideas like the one that prompted this inquiry still remain to be uncovered? There is only one way to find out.