An Introduction to the Action Chunking Transformer

This is a gentle introduction to training two robotic arms using transformers. If you would rather jump straight into code, please find a batteries-included notebook here.

Humans have figured out how to do a lot of neat and useful things.

Wouldn't it be great if we could teach some of them to our robots?

Enter the field of imitation learning which deals with exactly this problem – given an expert demonstration of for instance replacing a battery or cooking a meal, how do we get a machine to reproduce it?

The Action Chunking Transformer is a seminal and fascinating work in that space that achieves the above-stated goal leveraging the strengths of the transformer architecture.

On top of that, the authors do their research in the open, sharing their code and data with us!

This presents a unique learning opportunity to peer into the world of robotics and to better understand the powerful friend we keep running into wherever we turn these days – the transformer!

Let's dive in.

The problem statement

We are presented with two robotic arms. Each has 6 degrees of freedom plus a gripper that can open and close.

The moving parts of a robot are called actuators – usually, they are very precise rotary servo motors.

Since all a servo can do is revolve by up to 360 degrees, we can describe its position by a single number that reflects how far into its rotation it is.

So how do we control a robot?

We give a number to an actuator telling it where we want it to go! That's it.

And if we poll the robot for the revolution of all of its actuators – we get the current state of the robot!

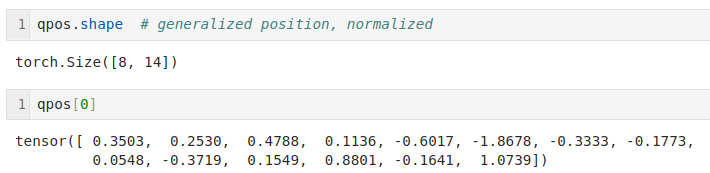
From readings to movement

We now know how to describe the position of a robot, but how do we describe movement?

The only thing we are missing is projecting the state of the robot across time.

To describe the motion of a robot arm, we take readings spaced by some interval of time, for example, 50 times a second (at 50hz).

So if we had a human operating a robotic arm for 5 seconds, we could capture the movement as a matrix of shape 50 by 14 containing the position of the arms at 0.02s intervals.

In the screenshot above a human is driving replicas of the robotic arms. The actuators in those arms don't generate movement, rather, they take 14 readings 50 times a second (6 actuators per arm + one reading describing the state of the gripper, 7 multiplied by 2 for two arms gives us 14 numbers).

By sending the arms their goal position 50 times a second we create the trajectory the arms travel on.

And by sending these coordinates from leader to follower arms we control the movement! (and record data to train on in the process )

At every time step, we also capture an image from a camera (or multiple cameras) that we will use to train the robot.

We present this information to a neural network – that is, we show it the target position of the arms at the current time step t along with an image of the current state and hope that it will be able to predict the target states of the robot at time steps t+1 up to t+n (where n is the chunk size, hence Action Chunking Transformer!)

And as we send those predictions to the robot every 0.02s, voila! We create movement!

So how do we go from this high-level description to modeling this task in a manner tractable to a neural network?

This is what we'll look at next.

The Action Chunking Transformer in all its ingenuity

This section might be a bit harder to follow due to all the technical details that are not easy to convey with words. Do not worry if you don't understand everything fully at first read. Also, if you are a bit rusty on the transformer architecture, I would highly recommend reading this fabulous blog post by Benjamin Warner on the various types of attention. It might also be easier to understand what is going on by alternating between reading this blog post and looking at the actual code.

The following image from the Action Chunking Transformer paper and the description below provides the full story!

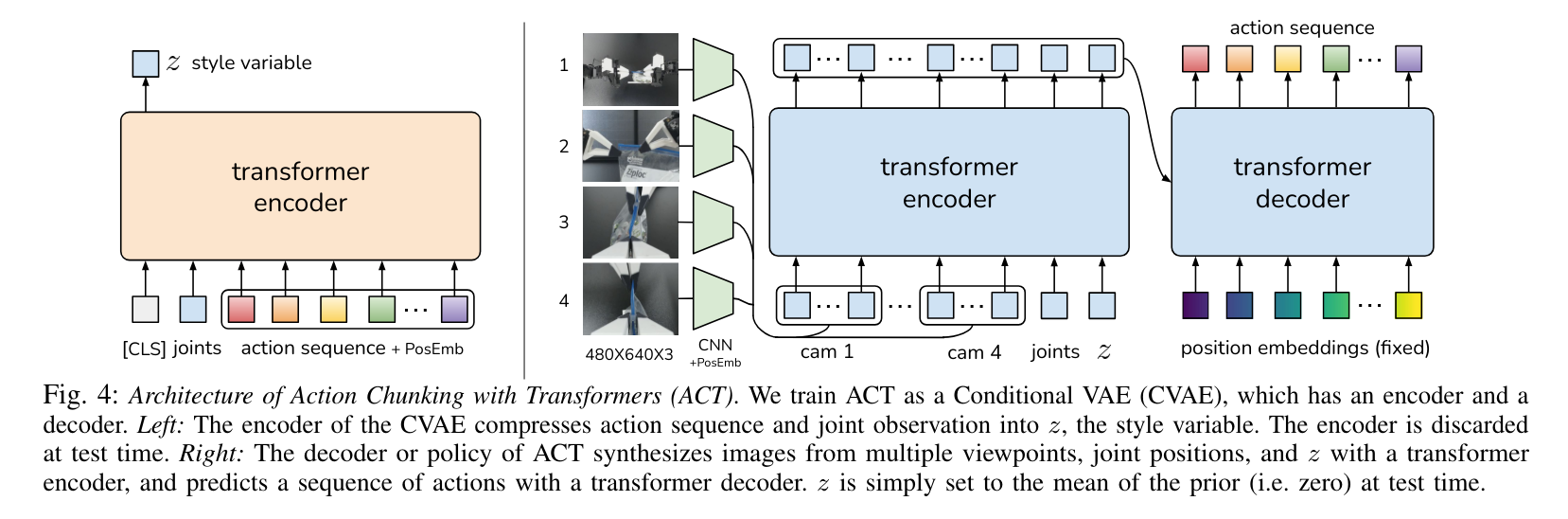
Unfortunately, it is not easy to unpack all that is happening here if you are not a researcher in robotics and have a thorough understanding of previous work.

So let's work step by step on what is happening.

The big picture is that we want to generate a sequence of actions. Those are the colorful boxes in the upper right-hand corner of the image

We show one or more pictures to the encoder-decoder transformer depicted in blue. As a first step, it represents the pictures as a set of feature maps (vector descriptors) using a standard CNN backbone with the classification head removed (the operation is depicted by the light green boxes alongside the images).

These feature maps are then reshaped so that we obtain some number of vectors (300 in the case of resnet18) that happen to be... in the shape of embeddings the encoder of our encoder-decoder transformer accepts!

We also pass it the current state of the robot represented by the 14 floats we discussed earlier.

So how do we feed the 1 by 14 vector into the model?!

We project it to the dimensionality of 512 using a single linear layer (or in other words, multiply it by a learnable matrix W).

We also pass in the style variable z, but let us not concern ourselves with it for now. We will come back to it in a second.

To recap, the encoder of our transformer takes in:

• some number of images
• current state of the model
• the style variable z

and outputs a bunch of embeddings. These embeddings represent the current state the decoder will tap into as it generates the action sequence.

So far so good – apart from embeddings not representing parts of sentences (tokens) but rather representing an image or a set of floats, this is standard transformer stuff.

But if we look at the decoder, the situation becomes more unusual.

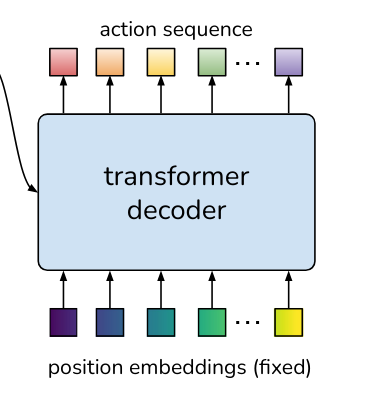
DETR to the rescue

What would normally go into the bottom of the decoder are word token embeddings from the text we are training the transformer to predict.

To liken the situation to the original transformer architecture, we could pass in a start of sequence token and then the embeddings of the actions to be predicted. This would frame the problem as a next-action prediction.

One limitation of this approach would be the need to use causal attention – that is, our model would only be able to consider the sequence up to t-1 when predicting the action at t.

Instead, the authors opted to ingeniously leverage the DETR (DEtection TRansformer) approach which, among other characteristics, allows the decoder to reason about the entire output sequence without the limitations of causal masking.

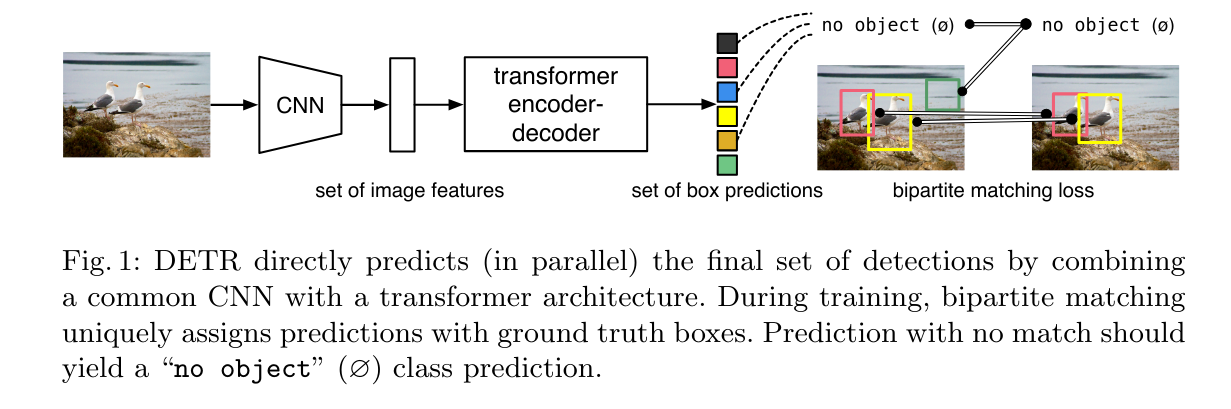
DETR is extremely exciting in its own right because it significantly streamlines and simplifies the machinery needed to do bounding box prediction.

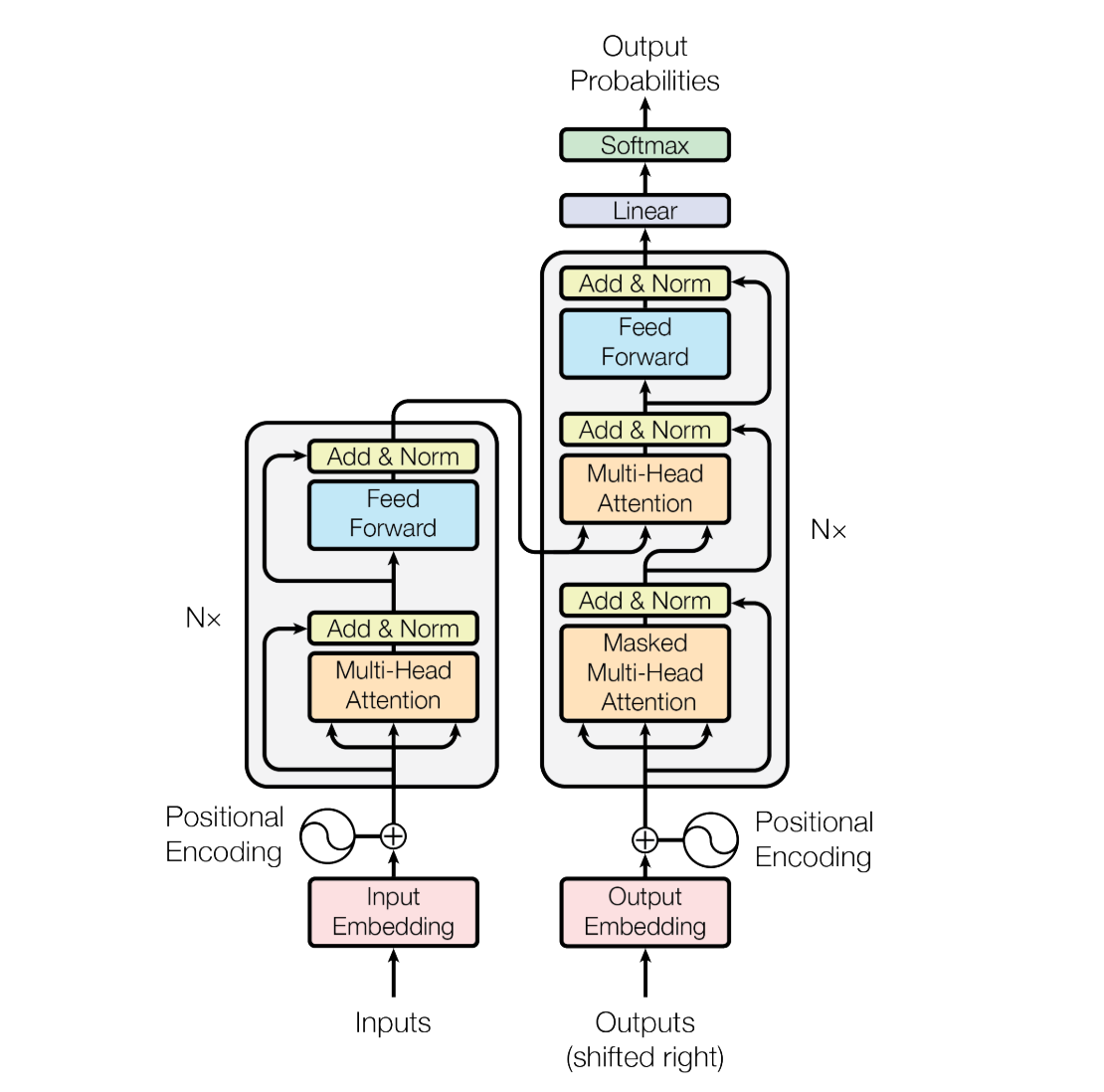
For reference here is a detailed diagram of the architecture:

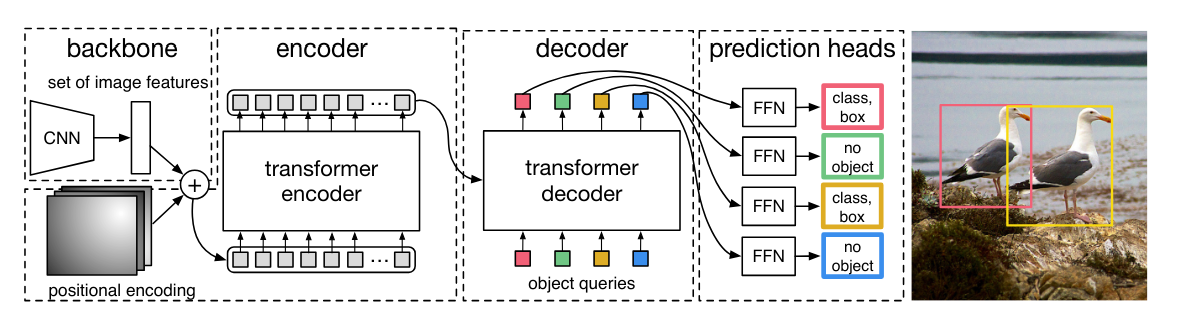
We have the CNN backbone again, we have the output of the encoder... and we also have the mysterious object queries going into the decoder!

In the case of DETR, these are learnable embeddings that stand for potential bounding boxes that the model can generate, with each embedding being different.

And in the case of the Action Chunking Transformer, these queries represent the actions in the sequence we are predicting.

The queries are transformed as they travel up the decoder stack and come out as predicted actions for each of the chunk size time steps we are predicting!

We are not passing any ground truth information into the decoder (just the learnable query embeddings) and thus no need for causal masking! For the generation of each action, the decoder can consider both the earlier and subsequent actions it is predicting.

Now, and this is an implementation detail (but an important one), the pictures do not tell the entire story.

What gets passed into the decoder are not the queries themselves but rather a vector of all zeros (input values in the transformer parlance)!

At each decoder layer we have the standard Pytorch multihead attention and our query_embeddings get added to the zeros (and what they are mutated into as they travel up the stack) at every decoder layer!

tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
                           key=self.with_pos_embed(memory, pos),
                           value=memory, attn_mask=memory_mask,
                           key_padding_mask=memory_key_padding_mask)[0]

One nice aspect of this framing is that we get residual connections for free as the repeated addition operation helps with gradient propagation.

The troublesome style variable z

We now have nearly the entire story, if it weren't for the pesky variable z and the transformer encoder on the left.

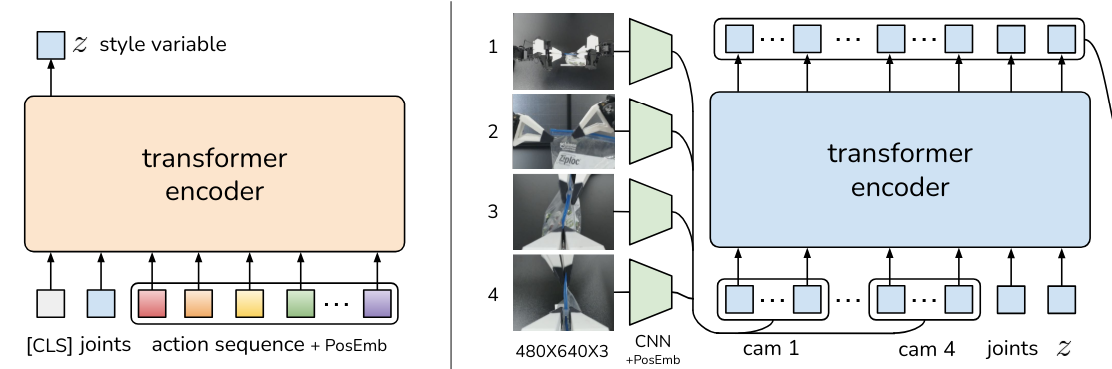
That encoder looks at the entire action sequence – the one we are attempting to predict, it compresses (some) of the information into the style variable z, which is then fed to the encoder of our encoder-decoder transformer on the right.

What does the style variable z accomplish?

It reframes the operation to a generation from a conditional variational autoencoder (or CVAE for short)!

We tell our encoder-decoder transformer (the one in blue):

Here, have these images and the current state of the robot, and generate a trajectory of actions that will succesfully accomplish a task at hand.

We condition the generation on the input data (images + robot state at time step t).

At the end, we look at the generated steps and compare them against the recorded actions and backpropagate the loss (which is simply the l1 distance calculated between actual and predicted coordinates).

BUT there is an infinite number of ways one can go about going from point A to point B in space – which is exactly what the robot is doing!

So how can we penalize the neural network for any trajectory choice that it makes?

Maybe another trajectory would work just as well?

This is where the style variable z comes into play.

The transformer encoder on the left is shown the entire sequence of actions we are predicting. It then compresses whatever it finds most useful into the limited space afforded by the style variable z (and the sampling mechanism that comes with it, but the details are secondary to the general idea here).

So as it has limited capacity to use, the hope is that it will package the bits of the trajectory (pun intended) that it might otherwise be unable to recover purely from images and the state of the actuators at the timestep t of the sequence.

The hope is that the style variable z  will capture the unique characteristics of the movement that define the specific trajectory the model is training on whereas the general characteristics of the movement will be learned (and reproduced) by the encoder-decoder transformer on the right.

For inference, we discard the encoder on the left, and instead of supplying a specific style variable z we provide the most general representation of it, which is a vector of all zeroes.

It is as if during inference we were saying to the encoder-decoder transformer – ok, you've seen so many unique trajectories, now all I care about is you getting me from point A to point B, I don't care about the quirkiness of a trajectory anymore.

And it works.

Chunk me a river (of actions, perhaps)

And works well it does.

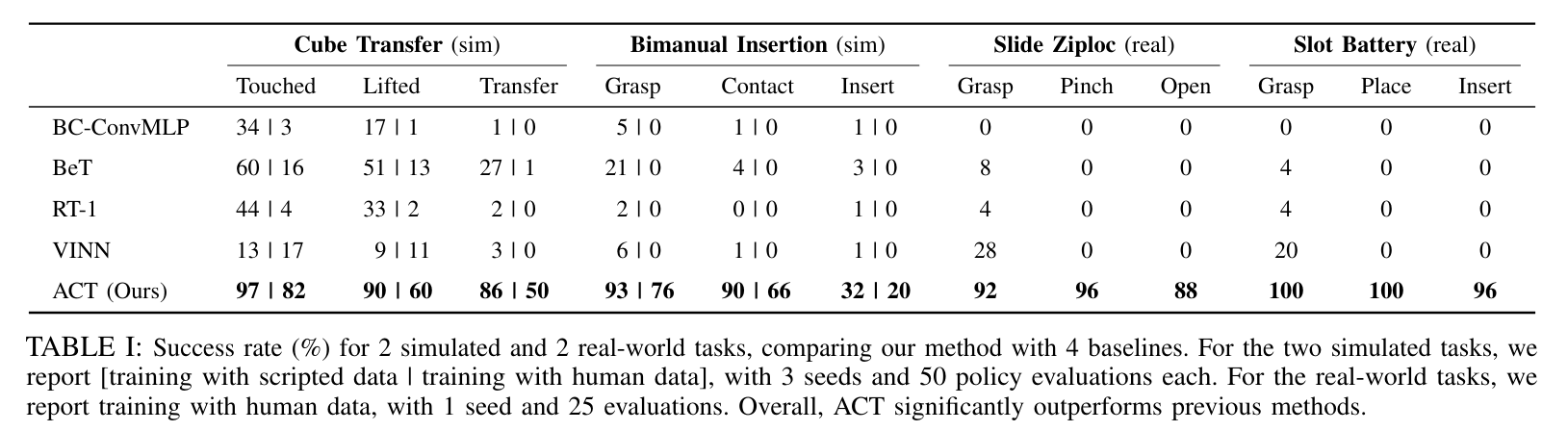
The disparity in performance between this and other methods is stunning and is a testament to this framing being the right abstraction for this particular problem (behavior cloning).

And yes, I do feel the choice of the transformer plays an important role here. Its ability to pick up on subtle patterns is unparalleled.

However, it is the combination of multiple ideas (like the style variable z discussed above) that makes this approach so potent.

Another such idea is that of chunking. What chunking means in this context is that when presented with a single observation the model predicts the next n steps.

And as we increase n to a certain point, the performance increases, not only for this method but also for others.

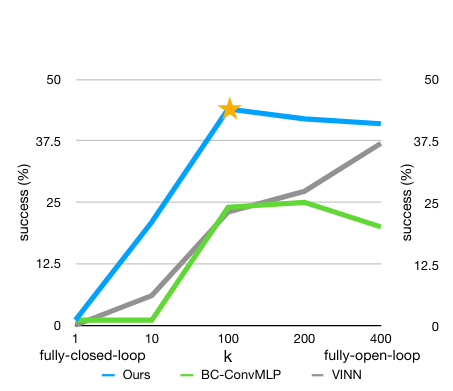
This is a stunning finding! An important piece of the puzzle.

The explanation of why it works goes something like this:

• from studying how humans process information, we know we "chunk" it into cohesive pieces
• it might be that the same phenomenon is taking place here – that it is "easier" for the neural network to operate on sequences of movements ("reaching out", "moving down", etc), than on the level of single, stand-alone movements (-1 degree on the z-axis, +0.5 on the x-axis, etc)

This is extremely intriguing to ponder, especially if we consider how many processes that we strive to predict are "chunkable" (price fluctuations, pressure readings, failure rates, resource utilization, and so on – the list is nearly endless).

All in all, I had a blast diving into the Action Chunking Transformer and am very grateful to the authors for the opportunity of going on this journey enabled by their choice to share their code!

I am extremely grateful to be able to add yet another powerful (and elegant) tool to my toolbox and thank you so much, dear reader, for accompanying me on this journey.

PS. In the time since writing this article till today (13 days!) LeRobot was released by HuggingFace. I feel there is a great need for a canonical implementation of robotics SoTA policies and I am very excited to see it take shape! I have implemented inferencing against ACT data from lerobot using a pretrained checkpoint trained using the code I developed for this blog post.

More importantly, please find a notebook here training an ACT model using only lerobot functionality. That is probably the best, top-down method for learning about, and training with, ACT.