Why take the log of a continuous target variable?
In this article, we’ll look at a simple but useful concept that often gets overlooked.

This blog post was originally published on Medium on 03/05/2018.
Data science is a conspiracy.
“Hi, my name is Bob and I’ll be your instructor. I’ll teach you how to drive a car. Open your books on page 147 and let’s learn about different types of exhaust manifolds. Here is the formula for the essential Boyle’s Law…”
This would never happen, right?
And yet in teaching data science elaborating on complex topics is commonplace whereas no love is given to the fundamentals. We are not told when to accelerate and when to slow down. But nearly everyone seems to be ready to walk us through the construction of real numbers.
In this article, we’ll look at a simple but useful concept that often gets overlooked. But first, let us consider an intriguing property of logarithms.
Addition is multiplication
Imagine you are a bubble in the World of Bubbles. You just started out and you are of meager size 0.69 which is equivalent to a natural log of 2.
You complete a quest for an NPC wizard who gives you a potion that will double your size, no matter how big you are.
That is nice. All the potion has to do is multiply your size by 2 to get your new size of 4. If you were of size 3, you would grow to 3 times 2 which is 6.
But what if the only operation a potion could do was addition? Now things become trickier. The wizard gives you a potion that grows your size by 2 from 2 to 4. But what if you drink the potion the next day, when you are already of size 3? 3 plus 2 is 5 and so the potion fails to deliver on its promise!
Seems like there is no solution to this. Luckily the wizard is very old and very wise. Instead of giving you a potion that adds 2 to your size, she gives you a potion that adds log(2).
You weigh the tiny flask in your hand not looking convinced. The wizard beams a bright smile at you and heads north-east.
You take the potion on the same day — you grow to size 4, as expected.
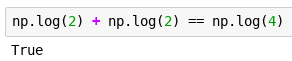
Not trusting the wizard, you load a save from before drinking the potion. To see what will happen you make a decision to drink it only once you reach size 3.
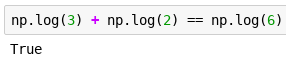
Mhmm, maybe the wizard anticipated that this is what you might do and set some timing mechanism into the potion, where after some time it would add 3 and not 2 to your size. You decide to throw the wizard a curveball.

Hmm.

What rules of magic apply to models?
Let’s consider random forests.
Imagine you look at a sword that your bubble can equip and would like to predict the power modifier based on its color and shape.
If sword blue -> add +2 to predicted power. If sword round, add -3.
A random forest can neither add nor subtract but what it learns has an effect like the rule above. When a tree is grown, it looks at the features of examples and selects which one to split on.
It attempts to group examples with similar values of the target variable together. The greater the similarity within a branch, the better the chance the tree will be able to make good predictions.
But how do we measure similarity? One way of going about it would be to consider how much the values differ in absolute terms — a 20$ bottle of wine is 20$ away from its 40$ counterpart. A 100$ bottle of whiskey is 100$ away from its 200$ counterpart.
Looking at the prices in this way, the difference between the bottles of whiskey is 5 times as big. But if we look at them in relative terms, the distances are the same! In both pairs, the second bottle is twice as expensive as the first one.
Neither way of measuring the similarity is universally better or worse. Depending on the situation, one might be more useful than the other.
The answer is in the question
Let’s imagine we would like to learn something about cars.
What might we want to know? Maybe for instance — how much will the value of a car increase if we fit it with AC?
As it turns out, we are very lucky — our dataset is simple and consists only of Lamborghinis and Fiats.

“Seems adding an AC to a Fiat on average will increase its price by 307$ and to a Lamborghini by 12 000$ so let me do the only reasonable thing here and predict that fitting AC to a car will increase its price by (12 000$ + 307$) / 2 = 6 153.50$”
But this would mean that if we equip a Fiat 126p with AC it will appreciate by multiples of its base price! Now that is a business I would like to be in.
Not a very good answer to say the least.
Alternatively, what if we ask by how much a car’s value will increase relative to its base price? This might be a more useful piece of information to have.
But our model is unable to answer this question! All it has are the absolute distances to go by.
Enter the wise wizard. After a single incantation of the numpy variety, our target variable becomes a logarithm.
Our model can now learn by what amount relative to a base price a car’s value will change based on adding or removing this or that feature.