How to fine-tune a Transformer (pt. 2, LoRA)

In part 1 of this series, I fine-tuned a Transformer using techniques straight from Universal Language Model Fine-tuning for Text Classification published in 2018.
But so much has happened in the last 5 years!
My plan was to read a couple of papers next, but I stumbled across LoRA: Low-Rank Adaptation of Large Language Models and couldn't help myself from trying it out!
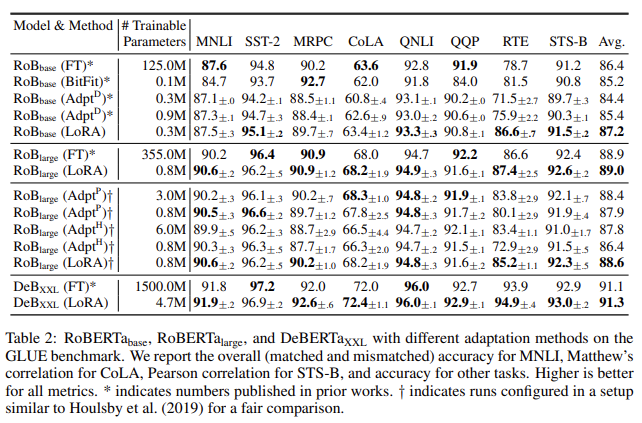
The results from the paper are very convincing – LoRA can often match or surpass full model fine-tuning (FT) and can reduce required VRAM by as much as 4x!
So what is it all about? And will I be able to get it to work on my data?
A brief intro to LoRA
LoRA springs from a fascinating observation that while modern neural networks contain many parameters, they can be optimized over a much smaller parameter space and still achieve good performance!
Here is how it all works.
Say we have a neural network with 199 210 parameters.
We can then randomly initialize a smaller set of parameters, let's say 750, along with a randomly initialized projection matrix (P) of dimensionality 199 210 by 750.
If we multiply our projection matrix with our 750 parameters we obtain 199 210 values, which is exactly the number of parameters in our neural network!
This idea is formalized in the following excerpt:
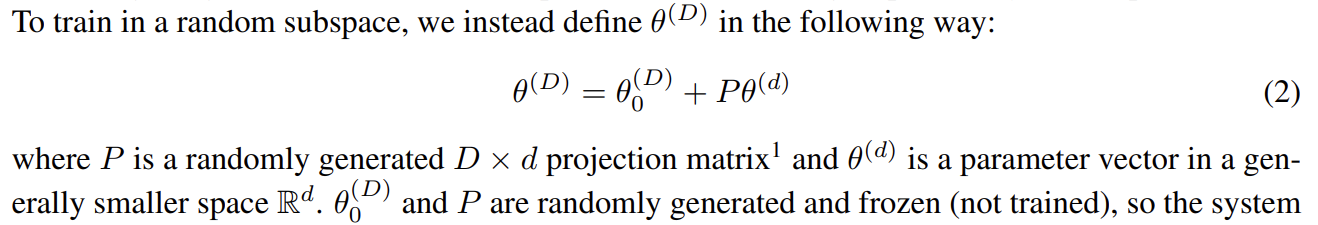
Once we project our 750 parameters to the full size of the network we can treat those values as deltas that we add to the full-size weights.
And that's it!
The big discovery is that this is enough to train our neural network to full performance.
That we don't need to backpropagate the loss with respect to the 199 210 weights but only with respect to the 750 parameters and we still end up with a model that performs well.
To summarize:
- if we randomly initialize our neural network
- randomly initialize a projection matrix
P - and only train the 750 parameters
our neural network will reach 90% of its performance as if we optimized all of the 199 210 parameters!
And on top of that, as we scale the 750 parameters up and down, we can achieve a desired level of performance (up to 100% of the 199 210 parameter network) while needing much less of GPU memory!
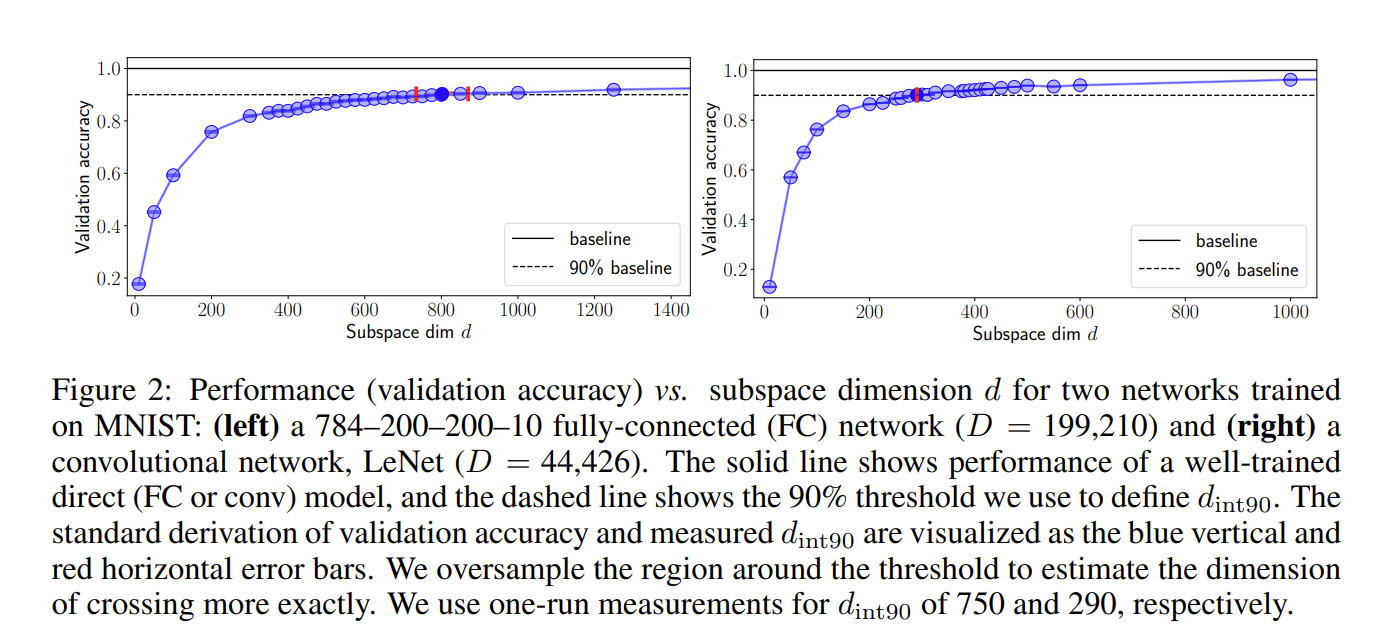
This is very surprising!
On one hand, we need our neural networks to have a high parameter count to achieve good performance, but on the other, we only need to train them over a much smaller parameter space!
<sidenote>
There is an interesting corollary to all of this in the context of the "compressibility" of neural networks.
Do you remember Amiga intros from the 80s? People created stunning animations using as little as 4kb or 64kb of code. This relied on some very creative procedural generation:
Procedural generation was huge in the early demo scene days. Obviously you never shipped a texture with your 4kb intro, you had a generate it from code. It's cool to see that there has been lots of progress along those lines.
— tobi lutke (@tobi) October 27, 2019
Something similar is happening here.
All you have to do is specify a seed to generate the initial state of weights of your full neural network (199 210 parameters in total) and a projection matrix P. You then provide this seed along with 750 floats and are able to recover the full, trained neural net!
</sidenote>
So what is the essence of LoRA?
LoRA extends the reasoning above and proposes the following training procedure:
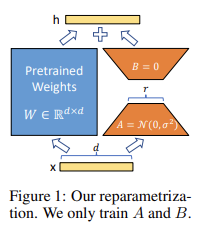
We begin with a starting state of weights (for instance, the pretrained weights of an LLM).
For every neural network layer that we chose to optimize, we decompose the weight matrix W into two smaller matrices A and B.
If we multiply B with A we obtain a matrix of the same dimensionality as W.
We train only by optimizing the much smaller matrices A and B.
But multiplied together, they produce a matrix that contains the deltas we add to our original weight matrix W and by doing so, we adapt our LLM to a new task!
This is the insight at the core of LoRA. It is formalized in the paper as follows:

The lora alpha that is mentioned above is also an interesting parameter, one that we will return to later.
And that's it!
As it turns out the r (which parametrizes the size of the decomposition matrices) can be extremely low (as compared to the size of the full weight matrix) and we still achieve very good performance!
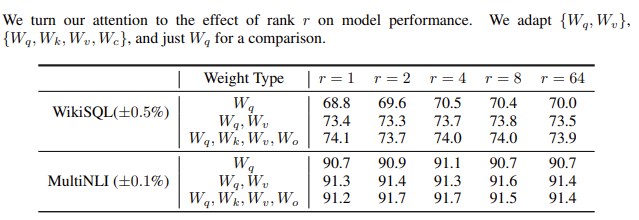
Another interesting observation made in the paper is that we don't need to optimize all weights in our Transformer.
Turns out that optimizing just the weight matrices of queries and values in the self-attention layers, and going as low as an r of 4 or 8, might be enough!
These are fascinating ideas – let's see whether we can put them into practice and get good results.
Experimentation
We will train on data for the Kaggle LLM Science Exam competition. For more information on the setup, please consult the first blog post in this series.
The baseline
We begin by training a baseline with all the weights of our neural network unfrozen.
Training time: 38 minutes
Trainable parameter count: 435 million
Mean map@3: 0.739
Now, before we jump to applying LoRA, can we attain a comparable performance by only fine-tuning the attention weights?
This was one of the ideas shared in the paper.
Initially, let's train all of the weight matrices in the attention layer, that is weight matrices for queries, keys, values and the output.
Training only the attention weights
Training time: 28 minutes
Trainable parameter count: 101 million
Mean map@3: 0.734
This works! 🙂 Unbelievable.
We maybe haven't reached the full performance, but what we have here is close enough.
Also, we trained with hyperparameters optimized for the training of the full model!
Maybe if we tweaked some of the hyperparameters we could reach better results?
But a bigger question is this– can we achieve comparable performance if we only train the weights for queries and values?
Training only the attention weights (query and value layers only)
Training time: 24 minutes
Trainable parameter count: 50 million
Mean map@3: 0.733
Wow, amazing!
This tells us something very important about how Transformers work that can be helfpul as we continue to study this architecture.
Time to unleash LoRA!
Training with LoRA and peft
We will use another of Hugging Face's fabulous libraries, peft (Parameter-Efficient Fine-Tuning).
Peft does the heavy lifting for us as it grabs the code from the MS LoRA paper repo and adapts it so that we can use it seamlessly with Hugging Face models.
What are the key parameters we can specify?
peft_config = LoraConfig(task_type="a_random_string", inference_mode=False, r=8, lora_alpha=32, lora_dropout=0.1)TaskType switches model classes but is not used for LoRA in any way AFAICT. Plus we are training a custom model, so we can safely get away with any value here.
r is the r we met in the paper – a key dimension of the A and B decomposition matrices. Specify a lower value – get smaller A and B and potentially less performance out of your model but at a smaller cost in VRAM.
lora_alpha is quite interesting. I hypothesized that maybe it is used to keep the parameter values in our As and Bs low to improve the dynamic range of our floats with 8-bit or 4-bit training, but that doesn't seem to be the case!
According to the paper, the objective here is to reduce the need to alter the hyperparams (when optimizing with Adam) when we change r. Makes our life easier!

lora_dropout is just good old dropout but applied to the weight matrix before we combine it with the result of B@A.
And that should be it!
But will it train? 🤔
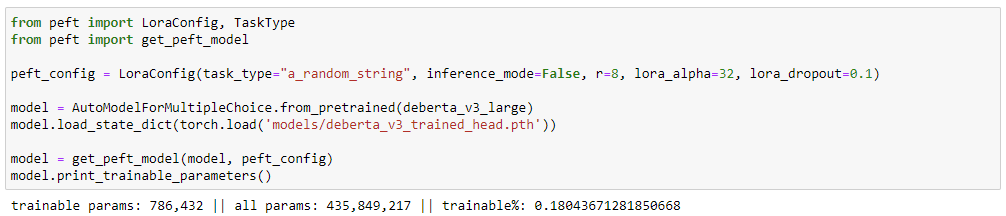
peft! 🤗) to transform our model into a LoraModelTraining time: 28 minutes
Trainable parameter count: 0.786 million
Mean MAP@3: 0.694
Only 786 432 trainable parameters, which is great, but our performance doesn't look good at all!
I trained with an lr of 1e-5 and I suspect it might be an order of magnitude or two too small.
But let's put this to a test.
Let us train with a lora_alpha of [8, 32, 128, 512, 1024] and see what we get.
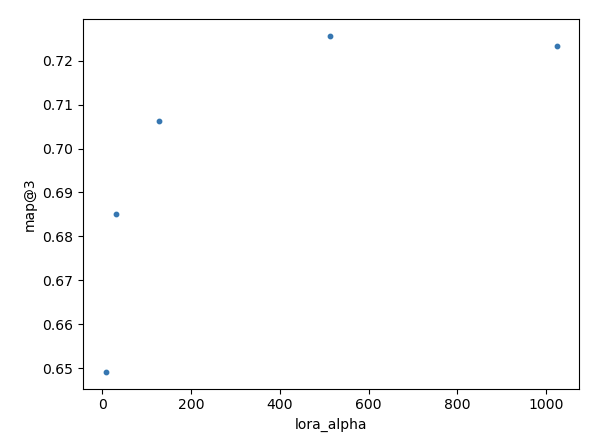
At a lora_alpha of 512 we reach the best performance of map@3 of 0.726!
And we could probably squeeze even more out of this method with fruther hyperparameter search!
Summary
LoRA is outstanding because it allows you to fine-tune models of gargantuan sizes on commodity hardware!
With the current architectures, you can expect a 1.3 billion parameter model to perform better than a 450 million parameter one, a 7 billion parameter model to perform better than a 1.3 billion parameter one, and so on.
And we now have a method that allows us to adapt much larger, much more capable models, to any downstream task of our choosing!
Of course, there is a bit of controversy – does this method really work that well?
How well can we combine it with other parameter-efficient optimization methods?
Okay I want comprehensive, conclusive answers on QLora, Lora, and Full Finetune.
— Teknium (e/λ) (@Teknium1) August 10, 2023
I propose we do the following:
- Pick 3 datasets, a LIMA Style dataset, a Larger Dataset like Hermes/Wizard/Orca, and a Task-Specific Dataset to train a qlora, lora, and full finetune with.
- Do…
But to me, LoRA is a dream come true!
First of all, it is extremely interesting from a theoretical perspective.
And secondly, I am very much looking forward to fine-tuning architectures that until very recently have been out of reach for me given my hardware 🙂
If techniques like LoRA are what the era of the Transformer has to offer, I am all for it!
In fact, I can't wait for what happens next.
Additional references:
A very interesting tidbit from the wonderful QLoRA: Efficient Finetuning of Quantized LLMs paper on how to optimize the performance of LoRA:

Two fantastic papers that inspired LoRA, highly recommended reads: